Uživatelské nástroje
Postranní lišta
 Přidat stránku do knihy
Přidat stránku do knihy  Odebrat stránku z knihy
Odebrat stránku z knihy Obsah
Pohyb tekutin
Ideální tekutina
Ideální tekutinou je látka umožňující proudění bez vnitřního odporu (supratekutost).
Chování této látky popisuje zjednodušeně věda pomocí těchto (Eulerových) rovnic v daném bodě 3D prostoru a čase:
- $-\nabla p=\rho\frac{Dv}{Dt}=\rho(\frac{\partial v}{\partial t}+(v\cdot\nabla)v)$
- Popisuje proudění
- Prostorový pokles tlaku způsobuje časové zrychlení „částice“
- $p$ je tlak (skalár)
- $v$ je rychlost proudění (vektor)
- $\rho$ je hustota hmotnosti (skalár)
- $\frac{Dv}{Dt}$ je celková časová změna rychlosti proudící „částice“ (materiálová derivace rychlosti podle času) (vektor)
- $\frac{\partial v}{\partial t}$ je časová změna rychlosti v bodě (částečná derivace rychlosti podle času) (vektor)
- $\nabla{v}$ je prostorová změna rychlosti v bodě (bivektor)
- $\cdot$ je vnitřní násobení (skalární součin) vektorů
- $(v\cdot\nabla)v$ je prostorová změna rychlosti ve směru (a velikosti) rychlosti (vektor)
- $\nabla p$ je prostorová změna tlaku (gradient - směr a velikost růstu vzhledem k okolí) (vektor)
- $\nabla\cdot(\rho v)=-\frac{\partial \rho}{\partial t}$
- Popisuje zachování hmotnosti
- To, co odchází z bodu do prostoru, způsobuje pokles hustoty v čase
- $\nabla\cdot(\rho v)$ je zřídlovost (divergence či vznik) toku hmotnosti v bodě (skalár)
Změny rychlosti proudění v prostoru $\nabla v$ můžeme rozdělit na symetrickou část divergenci/konvergenci (expanzi/smršťování) a deformaci a nesymetrickou část točení/rotaci. 1) Tomu pak odpovídá rozšířený popis proudění pomocí tenzorové algebry, tzv. nelineární mechanika kontinua. 2)
Celkově ale narážíme na omezené pochopení hmotností bez duchovních příčin. Není známá podstata hmotnosti, elektřiny a magnetismu apod., jen existuje jejich částečný popis.
Navíc i popis pohybu proudění tekutin naráží na nesrovnalosti a tedy ho lze stále zlepšovat, což se týká i nesrovnalostí v používaných matematických popisech.
- Peng Shi
- J. Tinsley Oden
Stlačitelná tekutina
Někteří považují éter za ideální plyn, který jde stlačit čili je pružný podobně jako vzduch. Navíc pokud má i tření, vzniká odpor brzdící proudění, tzv. viskozita.
Považuji takové vlastnosti za vyvinuté z ideální tekutiny éteru pomocí vířivých pulzujících proudů.
- James Clerk Maxwell
Proudění s nejmenším odporem
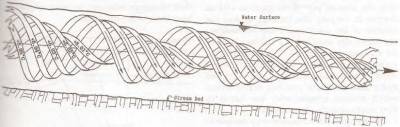
Beltramiho proudění
- Theophanes E. Raptis, Christos D. Papageorgiou
- Pavel Bělík, Xueqing Su, Douglas P. Dokken, Kurt Scholz, Mikhail M. Shvartsman
- Don Reed
- Peter Constantin, Andrew Majda
-
- každé proudění nestlačitelné tekutiny je sloučením Beltramiho proudění
-
- Viktor Schauberger
- Viktor Trkal
Relativita
Obecná teorie relativity zavádí časoprostor, zakřivení prostoru hmotou a pohyb po geodetikách, čili nejkratši cestou, zobecněnou „přímkou“ v zakřiveném prostoru. To je také pohyb s nejmenším odporem, ale „zakřivení prostoru“ je dané právě prouděním.
-
-
- Odhalení popisu obecné teorie relativity jako deformace spojitého prostředí (ideální tekutiny)
-
- Viskozita tekutého prostoročasu (éteru): Cesta ke sjednocení fyziky (Liquid Spacetime (Aether) Viscosity: A Way to Unify Physics + kopie)
- Porovnání obecné teorie relativity a kvantové mechaniky: jejich rovnice popisují viskózní tekutý éter pohybující se cestou nejmenšího odporu.

 Zobrazit/upravit knihu (
Zobrazit/upravit knihu ( Nápověda
Nápověda